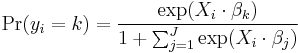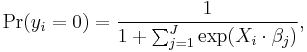Multinomial logit

In statistics, a multinomial logit (MNL) model, also known as multinomial logistic regression, is a regression model which generalizes logistic regression by allowing more than two discrete outcomes.^[1] That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables (which may be real-valued, binary-valued, categorical-valued, etc.).

In some fields of machine learning (e.g. natural language processing), when a classifier is implemented using a multinomial logit model, it is commonly known as a maximum entropy classifier, or MaxEnt model for short. Maximum entropy classifiers are commonly used as alternatives to Naive Bayes classifiers because they do not assume statistical independence of the independent variables (commonly known as features) that serve as predictors. However, learning in such a model is slower than for a Naive Bayes classifier. Nevertheless, it is well-known that using lasso can bring a highly efficient sparse solution. In particular, learning in a Naive Bayes classifier is a simple matter of counting up the number of cooccurrences of features and classes, while in a maximum entropy classifier the weights, which are typically maximized using maximum a posteriori (MAP) estimation, must be learned using an iterative procedure; see below.

1 Introduction
2 Assumptions
3 Model
4 Estimation of intercept
5 Applications
6 See also
7 References

Introduction

Multinomial logit regression is used when the dependent variable in question is nominal (a set of categories which cannot be ordered in any meaningful way, also known as categorical) and consists of more than two categories. For example, multinomial logit regression would be appropriate when trying to determine what factors predict which major college students choose.

Multinomial logit regression is appropriate in cases where the response is not ordinal in nature as in ordered logit. Ordered logit regression is used in cases where the dependent variable in question consists of a set number (more than two) of categories which can be ordered in a meaningful way (for example, highest degree, social class) while multinomial logit is used when there is no apparent order (e.g. the choice of muffins, bagels or doughnuts for breakfast) .

Assumptions

The multinomial logit model assumes that data are case specific; that is, each independent variable has a single value for each case. The multinomial logit model also assumes that the dependent variable cannot be perfectly predicted from the independent variables for any case. As with other types of regression, there is no need for the independent variables to be statistically independent from each other (unlike, for example, in a Naive Bayes classifier); however, collinearity is assumed to be relatively low, as it becomes difficult to differentiate between the impact of several variables if they are highly correlated.

If the multinomial logit is used to model choices, it relies on the assumption of independence of irrelevant alternatives (IIA) which is not always desirable. This assumption states that the odds do not depend on other alternatives that are not relevant (e.g. the relative probabilities of taking a car or bus to work do not change if a bicycle is added as an additional possibility). The IIA hypothesis is a core hypothesis in rational choice theory; however numerous studies in psychology show that individuals often violate this assumption when making choices. An example of a problem case arises if choices include a car and a blue bus. Suppose the odds ratio between the two is 1 : 1. Now if the option of a red bus is introduced, a person may be indifferent between a red and a blue bus, and hence may exhibit a car : blue bus : red bus odds ratio of 1 : 0.5 : 0.5, thus maintaining a 1 : 1 ratio of car : any bus while adopting a changed car : blue bus ratio of 1 : 0.5. Here the red bus option was not in fact irrelevant, because a red bus was a perfect substitute for a blue bus.

If the multinomial logit is used to model choices, it may in some situations impose too much constraint on the relative preferences between the different alternatives. This point is especially important to take into account if the analysis aims to predict how choices would change if one alternative was to disappear (for instance if one political candidate withdraws from a three candidate race). Other models like the nested logit or the multinomial probit may be used in such cases as they need not violate the IIA.

Model

Let there be dependent variable categories 0, 1, ..., J with 0 being the reference category. One regression is run for each category 1, 2, ..., J to predict the probability of y_i ( the dependent variable for any observation i) being in that category. Then the probability of y_i being in category 0 is given by the adding-up constraint that the sum of the probabilities of y_i being in the various categories equals one. The regressions are, for k = 1, 2, ..., J:

$\Pr(y_{i}=k)=\frac{\exp(X_{i} \cdot \beta_{k})}{1%2B\sum_{j=1}^{J}\exp(X_{i} \cdot \beta_{j})}$

and to ensure satisfaction of the adding-up constraint,

$\Pr(y_{i}=0)=\frac{1}{1%2B\sum_{j=1}^{J}\exp(X_{i} \cdot \beta_{j})},$

where y_i is the observed outcome for the ith observation on the dependent variable, X_i is a vector of the ith observations of all the explanatory variables, and β_j is a vector of all the regression coefficients in the jth regression. The unknown parameters in each vector β_j are typically jointly estimated by maximum a posteriori (MAP) estimation, which is an extension of maximum likelihood using regularization of the weights to prevent pathological solutions (usually a squared regularizing function, which is equivalent to placing a zero-mean Gaussian prior distribution on the weights, but other distributions are also possible). The solution is typically found using an iterative procedure such as iteratively reweighted least squares (IRLS) or, more commonly these days, a quasi-Newton method such as the L-BFGS method.

Estimation of intercept

When using multinomial logistic regression, one category of the dependent variable is chosen as the reference category. Separate odds ratios are determined for all independent variables for each category of the dependent variable with the exception of the reference category, which is omitted from the analysis. The exponential beta coefficient represents the change in the odds of the dependent variable being in a particular category vis-a-vis the reference category, associated with a one unit change of the corresponding independent variable.

Applications

Random multinomial logit models combine a random ensemble of multinomial logit models for use as a classifier.

References

^ Greene, William H., Econometric Analysis, fifth edition, Prentice Hall, 1993: 720-723.